
Thus, two processors that meet the IEEE 754 specification could produce slightly different results for the same computation if they were set to use different rounding methods. The IEEE 754 standard requires that the round toward the nearest is the default rounding method, and that the others be available for the user to select. An exponent of all 1’s and any non-zero significand indicates a value of Nan. The sign-bit denotes either the value is ±∞ or −∞. Infinity also has a significand equal to 0 but its exponent has every bit set to 1. The significand also includes an implied. Single precision numbers have 32 bits 1 for the sign, 8 for the exponent, and 23 for the significand. The IEEE 754 standard specifies two precisions for floating-point numbers. The value 0 has a significand equal to 0 and an exponent with all bits set to 0. For example, a CPU can meet the standard whether it uses shift-add hardware or the Wallace tree to multiply two significant. Zero,±∞, and Nan have predefined representations in both single and double precision formats. The exponent is stored as 4 + bias, or 4 + 1023 = 1027, for this value. Table (b) shows the representation of +19.5 in double precision format. The smallest and largest exponent values, -1023 and +1024 are reserved for special numbers. The exponent has a bias of 1023 and a range value from -1022 to +1023. As in single precision, the significand has an implied leading 1 for most values.
IEEE 754 FP STANDARD CALCULATOR 64 BITS
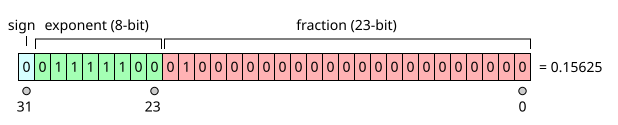
Exponent 4 is represented as 1000 0011, or 131, due to the addition of the bias of 127.ĭouble precision numbers use 64 bits − 1 for the sign, 11 for the exponent, and 52 for the significand. The leading 1 is not included in the significand, its presence is implicit in this standard. Table (a) shows the representation of +19.5 (=10011.1 or 1.00111 x 2 4 in binary) in single-precision format. The significand also includes an implied 1 to the left of its radix point. Single precision numbers have 32 bits − 1 for the sign, 8 for the exponent, and 23 for the significand.
For example, a CPU can meet the standard whether it uses shift-add hardware or the Wallace tree to multiply two significant. This standard does not specify arithmetic procedures and hardware to be used to perform computations. All computers conforming to this standard would always calculate the same result for the same computation. This standard defines set formats and operation modes. IEEE developed the IEEE 754 floating-point standard.


 0 kommentar(er)
0 kommentar(er)
